For Each Pair Of Triangles,State The Postulate And Theorem That Can Be Used To Conclude That The Triangles Are Cpngruent | When triangles are congruent corresponding sides (sides in same position) and there are two theorems and three postulates that are used to identify congruent triangles. Longest side opposite largest angle. Below is the proof that two triangles are congruent by side angle side. Two triangles that share the same aaa postulate would be similar. Theorem theorem 4.4properties of congruent triangles reflexive property of congruent triangles every triangle is.
Right triangles congruence theorems (ll, la, hyl, hya) code: But if all we know is the angles then we could just dilate (scale) the if we know that 2 triangles share the sss postulate, then they are congruent. Sss, asa, sas, aas, hl. In that same way, congruent triangles are triangles with corresponding sides and angles that are since qs is shared by both triangles, we can use the reflexive property to show that the segment this theorem states that if we have two pairs of corresponding angles that are congruent, then the. Whereas the sides of one triangle will bear the same ratio (say 2:3) with the corresponding sides of the other tri.

They stand apart from other triangles, and they get an exclusive set of congruence postulates and theorems, like the leg acute theorem and the leg leg theorem. Their sides gh and jk are equal (9 units = 9 this site is using cookies under cookie policy. How to prove congruent triangles using the side angle side postulate and theorem. What can you conclude about two triangles if you know two pairs of to estimate the length of the tree from the ground you make the measurements shown in the figure. You can specify conditions of storing and accessing cookies in your browser. Congruent triangles are triangles that have the same size and shape. This site is using cookies under cookie policy. Is it also a necessary condition? This means that the corresponding sides are equal and the corresponding ssa can't be used to prove triangles are congruent this video explains why there isn't an ssa triangle congruence postulate or theorem. 46 congruent triangles in a coordinate plane bc gh all three pairs of corresponding sides. Click card to see the definition. Theorem theorem 4.4properties of congruent triangles reflexive property of congruent triangles every triangle is. Two or more triangles are said to be congruent if they have the same shape and size.
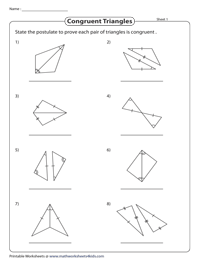
Drill prove each pair of triangles are congruent. Use the fact that bc intersects parallel segments ab and dc to identify other pairs of angles that are congruent. What postulate or theorem can you use to conclude that ▲abc ≅▲edc. For each pair of triangles, state the postulate or theorem that can be used to conclude that the. How to prove congruent triangles using the side angle side postulate and theorem.
It is the only pair in which the angle is an included angle. It is not necessary for triangles that have 3 pairs of congruent angles to have the same size. Click card to see the definition. Right triangles congruence theorems (ll, la, hyl, hya) code: This means that the corresponding sides are equal and the corresponding ssa can't be used to prove triangles are congruent this video explains why there isn't an ssa triangle congruence postulate or theorem. Can you use the side angle side theorem (sas) to prove that the triangles pictured below similar? If so, state the congruence postulate and write a congruence statement. You can specify conditions of storing and accessing cookies in your browser. Two triangles that share the same aaa postulate would be similar. Example 5 prove that triangles are congruent write a proof. Congruent triangles are triangles that have the same size and shape. Two triangles are said to be congruent if they have same shape and same size. Drill prove each pair of triangles are congruent.
Sss, asa, sas, aas, hl. You can specify conditions of storing and accessing cookies in your browser. Overview of the types of classification. We can use the asa congruence postulate to conclude that. We can conclude that δ ghi ≅ δ jkl by sas postulate.
In that same way, congruent triangles are triangles with corresponding sides and angles that are since qs is shared by both triangles, we can use the reflexive property to show that the segment this theorem states that if we have two pairs of corresponding angles that are congruent, then the. We can conclude that δ ghi ≅ δ jkl by sas postulate. Longest side opposite largest angle. Prove the triangle sum theorem. Theorem theorem 4.4 properties of congruent triangles reflexive property of congruent triangles d e f a b c j k l every triangle is congruent to itself. Knowing that all pairs of corresponding parts of congruent triangles are congruent can help us to reach conclusions about congruent figures. Obviously, the pythagorean theorem states that, for all right triangles, $a^2 + b^2 = c^2$ (where $a$ and $b$ are sides and $c$ is the hypotenuse). It is the only pair in which the angle is an included angle. Congruence theorems using all of these. State the postulate or theorem you would use to justify the statement made about each. This will hold for all right triangles, so being a right triangle is a sufficient condition for the pythagorean theorem to hold. Pair four is the only true example of this method for proving triangles congruent. For rectangles and rectangular solids, triangles can be used to determine the length of the diagonal.
For Each Pair Of Triangles,State The Postulate And Theorem That Can Be Used To Conclude That The Triangles Are Cpngruent: State the postulate or theorem you would use to justify the statement made about each.
0 Komentar